2023-04-17 09:25:47вАФ2023-04-17 09:25:47
–Ґ.–Ї. —Б–µ–є—З–∞—Б —П –≤ –Њ—З–µ–љ—М –љ–µ –њ—А–Њ–і—Г–Ї—В–Є–≤–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є –Є –љ–µ –Љ–Њ–≥—Г —З—В–Њ-—В–Њ –і–µ–ї–∞—В—М —Б–Є–ї—М–љ–Њ –≥–ї—Г–±–Њ–Ї–Њ–µ –Є –њ—А–Њ–і–Њ–ї–ґ–Є—В–µ–ї—М–љ–Њ–µ, –љ–Њ —В—П–≥–∞ –Є –Њ–≥–Њ–љ—М –Ї —Н—В–Њ–Љ—Г –≤–љ—Г—В—А–Є –µ—Й–µ –≥–Њ—А–Є—В. –ѓ —А–µ—И–Є–ї –њ–Њ–є—В–Є –љ–∞ —Е–Є—В—А–Њ—Б—В—М: —А–∞–Ј–±–Є—А–∞—В—М –±—А–Њ—И—О—А–Ї–Є –Ь–¶–Э–Ь–Ю, –≤ –Ї–Њ—В–Њ—А—Л—Е —Г—А–Њ–≤–µ–љ—М –Њ—В —Б—В–∞—А—И–Є—Е —И–Ї–Њ–ї—М–љ–Є–Ї–Њ–≤ –Є —Б—В—Г–і–µ–љ—В–Њ–≤ –Љ–ї–∞–і—И–Є—Е –Ї—Г—А—Б–Њ–≤. –С—А–Њ—И—О—А—Л —Д–Є–Њ–ї–µ—В–Њ–≤—Л–µ (–Ы–µ—В–љ—П—П —И–Ї–Њ–ї–∞ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–∞—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞) –Є –±–µ–ї—Л–µ. –Э–Њ –±—Г–і—Г—В –Є –і—А—Г–≥–Є–µ, –љ–∞–њ—А–Є–Љ–µ—А –њ–Њ –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є–Є –Є–ї–Є —В–µ–Њ—А–Є–Є –Ї–Њ–і–Є—А–Њ–≤–∞–љ–Є—П.

–Т–Њ—В —Б —Н—В–Њ–є –Є –љ–∞—З–љ—Г. –Ґ–µ–Љ –±–Њ–ї–µ–µ –Љ–љ–µ –Ї–∞–ґ–µ—В—Б—П –Њ—З–µ–љ—М –≤–∞–ґ–љ—Л–Љ —Б—В–Њ–ї–Ї–љ–Њ–≤–µ–љ–Є–µ –Ъ–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–Є –Є –Ґ–Њ–њ–Њ–ї–Њ–≥–Є–Є.
–Ґ–µ–Њ—А–µ–Љ–∞ –•–µ–ї–ї–Є.
–Э–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –≤—Б–њ–Њ–Љ–љ–Є—В—М –Є –Њ—Б–Њ–Ј–љ–∞—В—М –њ–Њ–љ—П—В–Є—П: –Т—Л–њ—Г–Ї–ї–Њ–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ, –Ј–∞–Ї—А—Л—В–Њ–µ (–Њ—В–Ї—А—Л—В–Њ–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ), –њ—А–µ–і–µ–ї—М–љ–∞—П —В–Њ—З–Ї–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞, –≤—Л–њ—Г–Ї–ї–∞—П –Њ–±–Њ–ї–Њ—З–Ї–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞, –≥–Є–њ–µ—А–њ–ї–Њ—Б–Ї–Њ—Б—В—М. (–Ґ—Г—В –Љ–Њ–ґ–µ—В –њ—А–Є–≥–Њ–і–Є—В—М—Б—П –Ї–љ–Є–≥–∞ –°–њ–µ–љ—М–µ—А–∞ "–≤–≤–µ–і–µ–љ–Є–µ –≤ —В–Њ–њ–Њ–ї–Њ–≥–Є—О", —В–∞–Љ –±—Л–ї–Є —А–∞—Б–Ї—А—Л—В—Л —Н—В–Є –њ–Њ–љ—П—В–Є—П) –Э—Г–ґ–љ—Л –µ—Й–µ –±–∞–Ј–Њ–≤—Л–µ –Ј–љ–∞–љ–Є—П –ї–Є–љ–µ–є–љ–Њ–є –∞–ї–≥–µ–±—А—Л. –Ф—Г–Љ–∞—О –њ–Њ–і–љ—П—В—М –Т–Є–љ–±–µ—А–≥–∞.
–Т—Л–њ—Г–Ї–ї–Њ–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –≤ –∞—Д—Д–Є–љ–љ–Њ–Љ –Є–ї–Є –≤–µ–Ї—В–Њ—А–љ–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ вАФ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ, –≤ –Ї–Њ—В–Њ—А–Њ–Љ –≤—Б–µ —В–Њ—З–Ї–Є –Њ—В—А–µ–Ј–Ї–∞, –Њ–±—А–∞–Ј—Г–µ–Љ–Њ–≥–Њ –ї—О–±—Л–Љ–Є –і–≤—Г–Љ—П —В–Њ—З–Ї–∞–Љ–Є –і–∞–љ–љ–Њ–≥–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞, —В–∞–Ї–ґ–µ –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—В –і–∞–љ–љ–Њ–Љ—Г –Љ–љ–Њ–ґ–µ—Б—В–≤—Г.
–Ь–µ–љ—П –±–µ—Б–њ–Њ–Ї–Њ–Є—В –≤–Њ–њ—А–Њ—Б –љ–µ–њ—А–µ—А—Л–≤–љ–Њ–≥–Њ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є—П. –Ъ–Њ–≥–і–∞ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В—М —В–Њ—З–µ–Ї –Њ—В–Њ–±—А–∞–ґ–∞–µ—В—Б—П, –љ–Њ –≤–Є–Ј—Г–∞–ї—М–љ–Њ "–Љ–µ–љ—М—И–∞—П" —Д–Є–≥—Г—А–∞ –њ–µ—А–µ—Е–Њ–і–Є—В –≤ "–±–Њ–ї—М—И—Г—О", —Е–Њ—В—П –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —В–Њ—З–µ–Ї –љ–µ –Є–Ј–Љ–µ–љ–Є–ї–Њ—Б—М. –Ґ.–µ. –Љ—Л —В—Г—В –љ–µ –њ—А–Њ —А–∞–Ј–Љ–µ—А—Л –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –Є–ї–Є –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞—Е. –°–Ї–ї–∞–і—Л–≤–∞–µ—В—Б—П –≤–њ–µ—З–∞—В–ї–µ–љ–Є–µ, —З—В–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ –Є–Љ–µ–µ—В –і–≤–∞ —Б–ї–Њ—П -- –і–Є—Б–Ї—А–µ—В–љ—Л–є (–Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–∞) –Є –љ–µ–њ—А–µ—А—Л–≤–љ—Л–є. –Ю—З–µ–љ—М –≥—А—Г–±–Њ–µ –Є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–љ–Њ–µ —Б—Г–ґ–і–µ–љ–Є–µ.
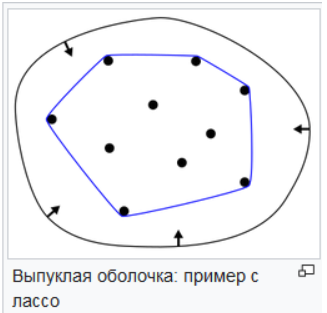
Conv (convex) -- –≤—Л–њ—Г–Ї–ї–∞—П –Њ–±–Њ–ї–Њ—З–Ї–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞. –Э–∞ –њ—А–Є–Љ–µ—А–µ: –Я—А–µ–і—Б—В–∞–≤—М—В–µ —Б–µ–±–µ –і–Њ—Б–Ї—Г, –≤ –Ї–Њ—В–Њ—А—Г—О –≤–±–Є—В–Њ вАФ –љ–Њ –љ–µ –њ–Њ —Б–∞–Љ—Г—О —И–ї—П–њ–Ї—Г вАФ –Љ–љ–Њ–≥–Њ –≥–≤–Њ–Ј–і–µ–є. –Т–Њ–Ј—М–Љ–Є—В–µ –≤–µ—А—С–≤–Ї—Г, —Б–≤—П–ґ–Є—В–µ –љ–∞ –љ–µ–є —Б–Ї–Њ–ї—М–Ј—П—Й—Г—О –њ–µ—В–ї—О (–ї–∞—Б—Б–Њ) –Є –љ–∞–±—А–Њ—Б—М—В–µ –µ—С –љ–∞ –і–Њ—Б–Ї—Г, –∞ –њ–Њ—В–Њ–Љ –Ј–∞—В—П–љ–Є—В–µ. –Т–µ—А—С–≤–Ї–∞ –Њ–Ї—А—Г–ґ–∞–µ—В –≤—Б–µ –≥–≤–Њ–Ј–і–Є, –љ–Њ –Ї–∞—Б–∞–µ—В—Б—П –Њ–љ–∞ —В–Њ–ї—М–Ї–Њ –љ–µ–Ї–Њ—В–Њ—А—Л—Е, —Б–∞–Љ—Л—Е –≤–љ–µ—И–љ–Є—Е. –Т —В–∞–Ї–Њ–Љ –њ–Њ–ї–Њ–ґ–µ–љ–Є–Є –њ–µ—В–ї—П –Є –Њ–Ї—А—Г–ґ—С–љ–љ–∞—П –µ–є –Њ–±–ї–∞—Б—В—М –і–Њ—Б–Ї–Є —П–≤–ї—П—О—В—Б—П –≤—Л–њ—Г–Ї–ї–Њ–є –Њ–±–Њ–ї–Њ—З–Ї–Њ–є –і–ї—П –≤—Б–µ–є –≥—А—Г–њ–њ—Л –≥–≤–Њ–Ј–і–µ–є
–Т –Њ—З–µ—А–µ–і–љ–Њ–є —А–∞–Ј –њ–Њ–і–Љ–µ—З–∞—О, —З—В–Њ –Љ–љ–Њ–≥–Њ –њ—А–Њ–±–ї–µ–Љ –Є –Ј–∞—В—Л–Ї–Њ–≤ –≤ –Є–Ј—Г—З–µ–љ–Є–Є –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –Є–Ј –Њ–±—Л—З–љ–Њ–є –љ–µ–≤–љ–Є–Љ–∞—В–µ–ї—М–љ–Њ—Б—В–Є. –Э–∞–њ—А–Є–Љ–µ—А, —П –љ–µ –Њ—З–µ–љ—М –≤–љ–Є–Љ–∞—В–µ–ї—М–љ–Њ –≤—З–Є—В–∞–ї –Є –Њ—Б–Њ–Ј–љ–∞–ї –Ґ–Њ–њ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї—Г—О —В–µ–Њ—А–µ–Љ—Г –†–∞–і–Њ–љ–∞. –Ш –≤ –Њ–±—А–∞–Ј–∞—Е –Љ—Л—Б–ї–Є–ї, —З—В–Њ —Б–Є–Љ–њ–ї–µ–Ї—Б –Є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –≤ –Ї–Њ—В–Њ—А–Њ–Љ –Њ–љ –Њ—В–Њ–±—А–∞–ґ–∞—О—В—Б—П –Њ–і–љ–Њ–є —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–Є. –І—В–Њ —З–µ–ї–Њ–≤–µ–Ї—Г –і–∞–ґ–µ —Б–Њ —Б–ї–µ–≥–Ї–∞ –љ–∞—А–∞–±–Њ—В–∞–љ–љ—Л–Љ–Є –Є–љ—В—Г–Є—Ж–Є—П–Љ–Є —Б—А–∞–Ј—Г –њ–Њ–Ї–∞–Ј–∞–ї–Њ—Б—М –±—Л –њ–Њ–і–Њ–Ј—А–Є—В–µ–ї—М–љ—Л–Љ.
–Я–µ—А–Љ—Г—В–Њ—Н–і—А. –Ь–љ–µ —Г–ґ–µ –љ—А–∞–≤–Є—В—Б—П —Н—В–Њ –љ–∞–Ј–≤–∞–љ–Є–µ. –£–≤–ї–µ–Ї—Б—П —З—В–µ–љ–Є–µ–Љ –≤ wiki –Ы–µ–Ї—Ж–Є–Є –У–∞—П–љ—Н –Я–∞–љ–Є–љ–Њ–є "–Ч–љ–∞–Љ–µ–љ–Є—В—Л–µ –Ь–љ–Њ–≥–Њ–≥—А–∞–љ–љ–Є–Ї–Є" yputube -- –Ї–∞–Ї —А–∞–Ј –њ—А–Њ –њ–µ—А–Љ—Г—В–Њ—Н–і—А (–Ї–∞–Ї –µ–≥–Њ –њ–Њ—Б—В—А–Њ–Є—В—М, –њ–∞—А—Г —Б–њ–Њ—Б–Њ–±–Њ–≤) –Ф–µ–ї–µ–љ–Є–µ –±–µ–Ј –Ј–∞–≤–Є—Б—В–Є –і–µ–љ—М—А–Њ–ґ–і–µ–љ–љ–Њ–≥–Њ –њ–Є—А–Њ–≥–∞ mathnet
–°–Ї–∞–ї—П—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ: –і–≤—Г—Е –љ–µ–љ—Г–ї–µ–≤—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –Є—Е –і–ї–Є–љ –љ–∞ –Ї–Њ—Б–Є–љ—Г—Б —Г–≥–ї–∞ –Љ–µ–ґ–і—Г –љ–Є–Љ–Є. ab = |a| ¬Ј |b| ¬Ј cos вИ†(a, b).


finished
–Т—Б–µ –Ј–∞–њ–Є—Б–Є